コレクション メンガースポンジ 182561-メンガースポンジ
「メンガーのスポンジ」のコンピュータグラフィックス アーサー・ケイリー と共に、 距離幾何学法 の基礎を築いたとされる。 特に直接測定できる 物理量 で(距離の比率として)角度と曲率の概念の定義を定式化した。メンガーのスポンジの次元は2より大きいため、2次元的な大きさである 面積 は無限である。 実際、表面積が1となる大きな立方体から穴を空けてメンガーのスポンジを構成する場合、一度穴を空ける毎にその表面積は 1 3 {\displaystyle {\tfrac {1} {3}}} 反復関数系 バーンズリーのシダ( 英語版 ) カントール集合 ドラゴン曲線 コッホ雪片 メンガーのスポンジメンガーのスポンジ メンガーのスポンジというのは、フラクタル図形の一つです。 メンガーのスポンジ Wikipedia;

Ulcamtcvsmps
メンガースポンジ
メンガースポンジ-メンガーのスポンジ めんがーのすぽんじ フラクタル構造の一例。正方形の立方体の6面すべてに、以下のように穴を開けていく。 1.中心部分に面積が1/9の正方形の穴を開ける。Cluster,Inc Advent Calendar 18、25日目の記事です。 qiitacom 概要 そろそろアドベントカレンダーのネタが切れてきたのたぐす(notargs)です。 フラクタルの勉強がしたかったので、Unityの簡単な機能だけを使ってメンガーのスポンジを作図してみました。 メンガーのスポン



メンガーのスポンジの内側の生活が奇妙な背景 の写真素材 画像素材 Image
メンガーのスポンジ メンガーのスポンジというのは、フラクタル図形の一つです。 メンガーのスポンジ Wikipedia;メンガーのスポンジ めんがーのすぽんじ フラクタル構造の一例。正方形の立方体の6面すべてに、以下のように穴を開けていく。 1.中心部分に面積が1/9の正方形の穴を開ける。メンガースポンジ レベル2 (1cmバージョン) その2 13年6月28日 (金) | コ (0), ト (0)
お父さんのCarl Mengerも国民経済学原理の出版で有名な経済学者なのでカール・メンガーで検索するとお父さんの方の業績が結構出てきるので混乱しないように注意です。 アイキャッチ画像は息子の業績である「メンガーのスポンジ(Menger sponge)」です。メンガーのスポンジ (Level4) 81mm x 81mmx 81mmの詳細。つくりたいもの、ほしいもの、ネットから3Dプリント!メンガースポンジ の記事一覧 ( 23 ) メンガースポンジ レベル3 (1cmバージョン)に着手 13年7月 2日 (火) | コ (0), ト (0) ;
メンガースポンジ レベル24 (1cmバージョン) その3 13年6月29日 (土) | コ (0), ト (0) ;↑メンガーのスポンジを斜めにカットした場合空洞化した部分が星形の断面図に見えるよね。Killing Bono Soundtrack Where We Wanメンガーのスポンジがイラスト付きでわかる! 「シェルピンスキーのカーペット」の三次元版ぽいの。 概要 フラクタル図形の一種であり、「シェルピンスキーのカーペット」を三次元化したような形。



The Strange Storage フラクタル図形をつくる


50 専用ユニット メンガースポンジ レベル2 Chimecocoのブログ
メンガーのスポンジで同じところを切ると、断面はどんな形になるだろう? — 盛田みずすまし (@nosiika) 年4月18日 まず最初の基本立体(レベル1、穴の無いただの立方体がレベル0)。 つづいてレベル2 次がレベル3 次がレベル4メンガースポンジ レベル2 (1cmバージョン) その2 13年6月28日 (金) | コ (0), ト (0)メンガーのスポンジはフラクタル図形であるため、正確に作図することはできない。 面積 メンガーのスポンジの次元は2より大きいため、2次元的な大きさである面積は無限である。 実際、表面積が1となる大きな立方体から穴を空けてメンガーのスポンジを構成する場合、一度穴を空ける毎に



メンジャースポンジ 3dモデル 45 Obj Fbx Dxf 3ds Max Free3d



Fractalの調べ 13 Memger S Sponge M0rya Site
メンガーのスポンジとは自己相似なフラクタル 図形の一種であり、立方体に穴をあけたものである。 そのフラクタル次元(ハウスドルフ次元、相似次元)は (= ) 次元である。 メンガーのスポンジの面は同じくフラクタル図形のシェルピンスキーのカーペットでできている。フラクタルな図形は、簡単な再帰で描画できるので、一時間位でコードを書き上げることが出来ました。 その結果がこれです。 綺麗ですね。 数学的に言うと、本当のメンガーのMenger sponge(メンガーのスポンジ)を描く Wikipediaから画像を引用させてもらうとこんな感じの絵。 また、文章では以下のように説明されています。 メンガーのスポンジとは自己相似なフラクタル図形の一種であり、立方体に穴をあけたものである。



三谷 純 Jun Mitani メンガーのスポンジ 関係で本日ツイートした画像13枚を ブログの方にまとめておきました メンガーのスポンジ みたにっき はてな T Co Mywcvy1ocr


48 園部式メンガースポンジ レベル2 Chimecocoのブログ
メンガーのスポンジとは自己相似なフラクタル 図形の一種であり、立方体に穴をあけたものである。 そのフラクタル次元(ハウスドルフ次元、相似次元)は (= ) 次元である。 メンガーのスポンジの面は同じくフラクタル図形のシェルピンスキーのカーペットでできている。第61問 メンガーのスポンジ 図形ドリル 6年生 フラクタル図形 投影図 立方体 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。メンガーのスポンジとは自己相似なフラクタル 図形の一種であり、立方体に穴をあけたものである。 そのフラクタル次元(ハウスドルフ次元、相似次元)は math\frac{\log}{\log3}(=\ldots)/math 次元である。 メンガーのスポンジの面は同じくフラクタル図形のシェルピンスキーのカーペットで



メンガーのスポンジの内側の生活が奇妙な背景 の写真素材 画像素材 Image



折紙 メンガーのスポンジlv 2 日常
成果物 wwwyoutubecom 今回は、有名なメンガーのスポンジの正四面体、正八面体バージョンを作ってみました。地味に正四面体、正八面体を描画するのも大変だったので、載せておきます。 正四面体の外接円の半径から、座標を求める式は難しかったので載せておきます。メンガーのスポンジを, 正三角錐をベースに作ったもの これは, 昔, vrml で作ったこともあったりした 立方体ベースのスポンジに比べて, 空隙 の部分が多いような気がして, スカスカな感じ 立体としての面白さよりも, 影のほうが趣があるメンガーのスポンジとは自己相似なフラクタル 図形の一種であり、立方体に穴をあけたものである。 そのフラクタル次元(ハウスドルフ次元、相似次元)は (= ) 次元である。 メンガーのスポンジの面は同じくフラクタル図形のシェルピンスキーのカーペットでできている。


壁紙をダウンロード フラクタル メンガーのスポンジ デスクトップの解像度のための無料壁紙 19x1080 絵 3031
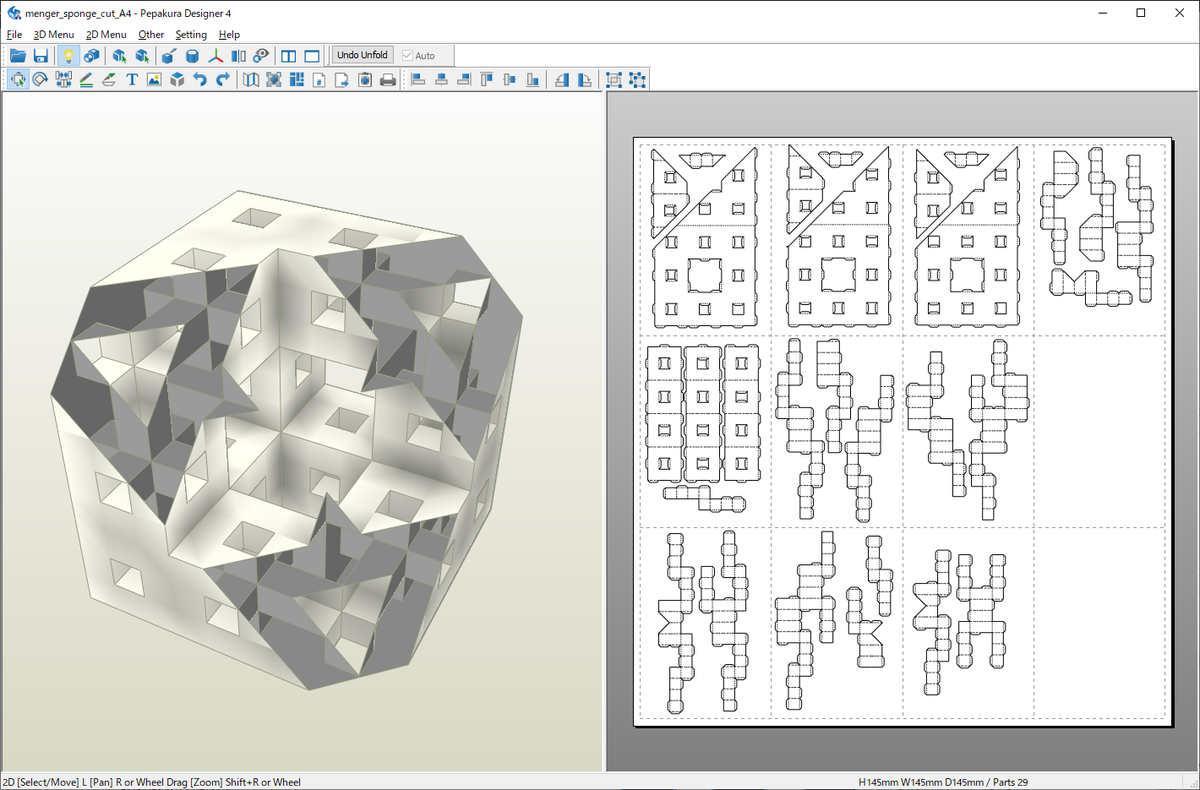


みたにっき はてな
メンガーのスポンジの表面積についてですが、自分が計算したところ、一辺1の立方体にn回穴開けた立体の表面積をSnと置くと、 Sn= (4*8ⁿ2*ⁿ)/9ⁿ になったのですが、Wikipediaには穴をあける ごとに表面積は4/3倍になると書いてありました。Cluster,Inc Advent Calendar 18、25日目の記事です。 qiitacom 概要 そろそろアドベントカレンダーのネタが切れてきたのたぐす(notargs)です。 フラクタルの勉強がしたかったので、Unityの簡単な機能だけを使ってメンガーのスポンジを作図してみました。 メンガーのスポン立方体の方は、メンガーのスポンジ といいます。 スポンジかぁ! そういえば、スポンジって、 食器洗い用の洗剤を閉じこめるためにも使っていたっけ。



Fractalの調べ 13 Memger S Sponge M0rya Site



フラクタルが熱い みんなが呟くフラクタルとは Togetter
メンガーのスポンジとは自己相似なフラクタル 図形の一種であり、立方体に穴をあけたものである。そのフラクタル次元(ハウスドルフ次元、相似次元)は (= ) 次元である。メンガースポンジ レベル24 (1cmバージョン) その3 13年6月29日 (土) | コ (0), ト (0) ;フラクタルな図形は、簡単な再帰で描画できるので、一時間位でコードを書き上げることが出来ました。 その結果がこれです。 綺麗ですね。 数学的に言うと、本当のメンガーの



折紙 メンガーのスポンジlv 2 日常



メンガーのスポンジ スチャラカでスーダラな日々
Menger sponge(メンガーのスポンジ)を描く Wikipediaから画像を引用させてもらうとこんな感じの絵。 また、文章では以下のように説明されています。 メンガーのスポンジとは自己相似なフラクタル図形の一種であり、立方体に穴をあけたものである。 そのフラクタル図形の例として 有名なこの図形を何という? シルピンスキーのギャスケット(答) フレイザー図形 メンガーのスポンジ リアプノフ・フラクタル 49% フラクタル(仏 fractale, 英 fractal)は、フランスの数学者ブノワ・マンデルブロが導入した幾何学の概念である。メンガースポンジ の記事一覧 ( 23 ) メンガースポンジ レベル3 (1cmバージョン)に着手 13年7月 2日 (火) | コ (0), ト (0) ;



Season6 Part60 投稿しました メンガーのスポンジです



メンジャースポンジmht 01 3dモデル 15 Obj Fbx Max Free3d


Yusuke Ogata Celestial Body7 16年11月10日のお気に入り ツイセーブ



フラクタルが熱い みんなが呟くフラクタルとは Togetter



折紙 メンガーのスポンジlv 2 日常



商品開発vtuberは便利グッズで世界を面白くする Vchase
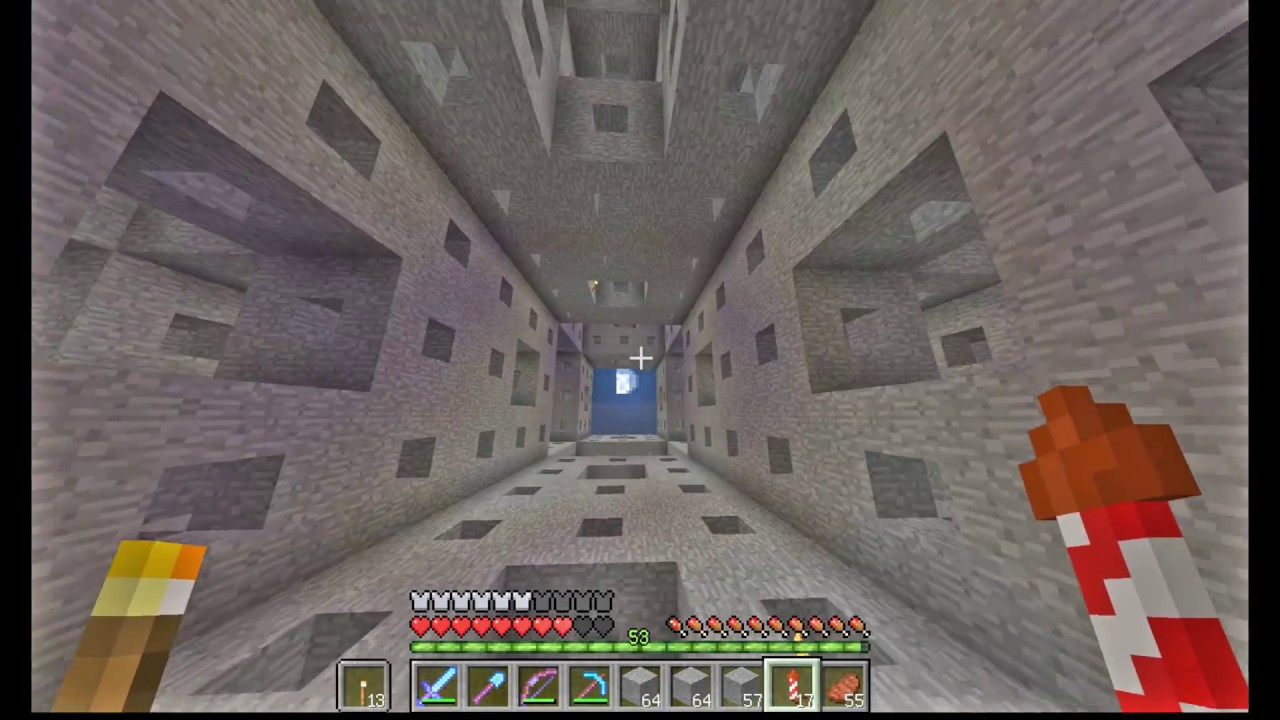


マインクラフトでメンガースポンジ作成 Youtube



有機 レンダリング フラクタル Pixabayの無料画像



3dモデル メンガーのスポンジ Fbx Megalo Arms Corp Booth



Minecraft 作りたくなったのでメンガ のスポンジ作った Youtube


Fredrikson Stallard Arkitexture



Fractalの調べ 13 Memger S Sponge M0rya Site


壁紙をダウンロード フラクタル マンデルブロ メンガーのスポンジ デスクトップの解像度のための無料壁紙 7686x5124 絵


Genesisゲーム内容案その1 Kengonakajima Note



Amazon Mtbblock Mathtime教育玩具diyおもちゃand Stem Toy For Children Lクリエイティブ学習の数学の図を使用して磁気ブロック アンチ メンガースポンジlevel1セット ままごと ごっこ遊び おもちゃ
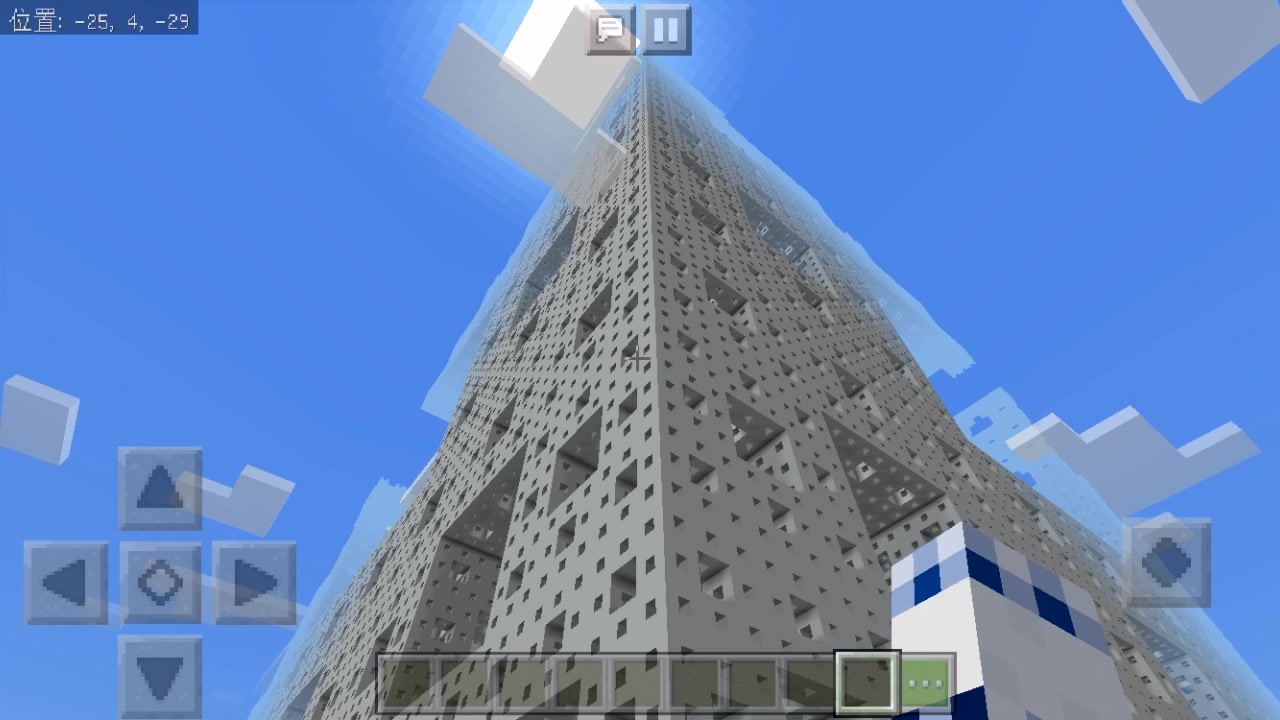


Minecraft 作りたくなったのでメンガーのスポンジ作った ニコニコ動画
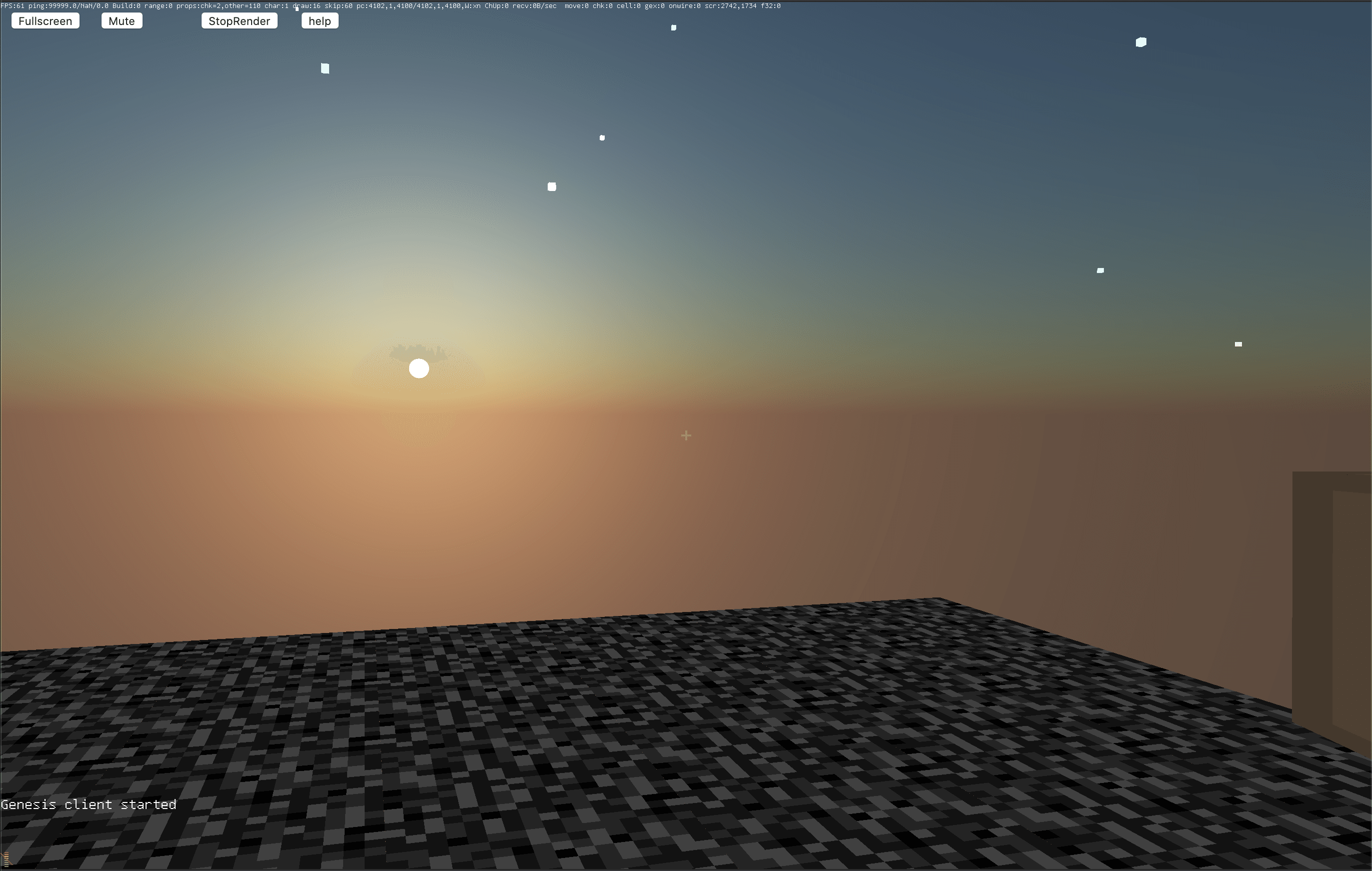


Mmorpgとは何か Kengonakajima Note



Processing 正四面体と 正八面体のメンガーのスポンジ Nekodigi S Diary



メンガーのスポンジ



Ulcamtcvsmps


Blog Mc Menger Sponge Md At Master Kengonakajima Blog Github



フラクタル


シェルピンスキーのギャスケット Wikipedia



シエルピンスキー3角形 Sgk Note



Ghp Prog Raham
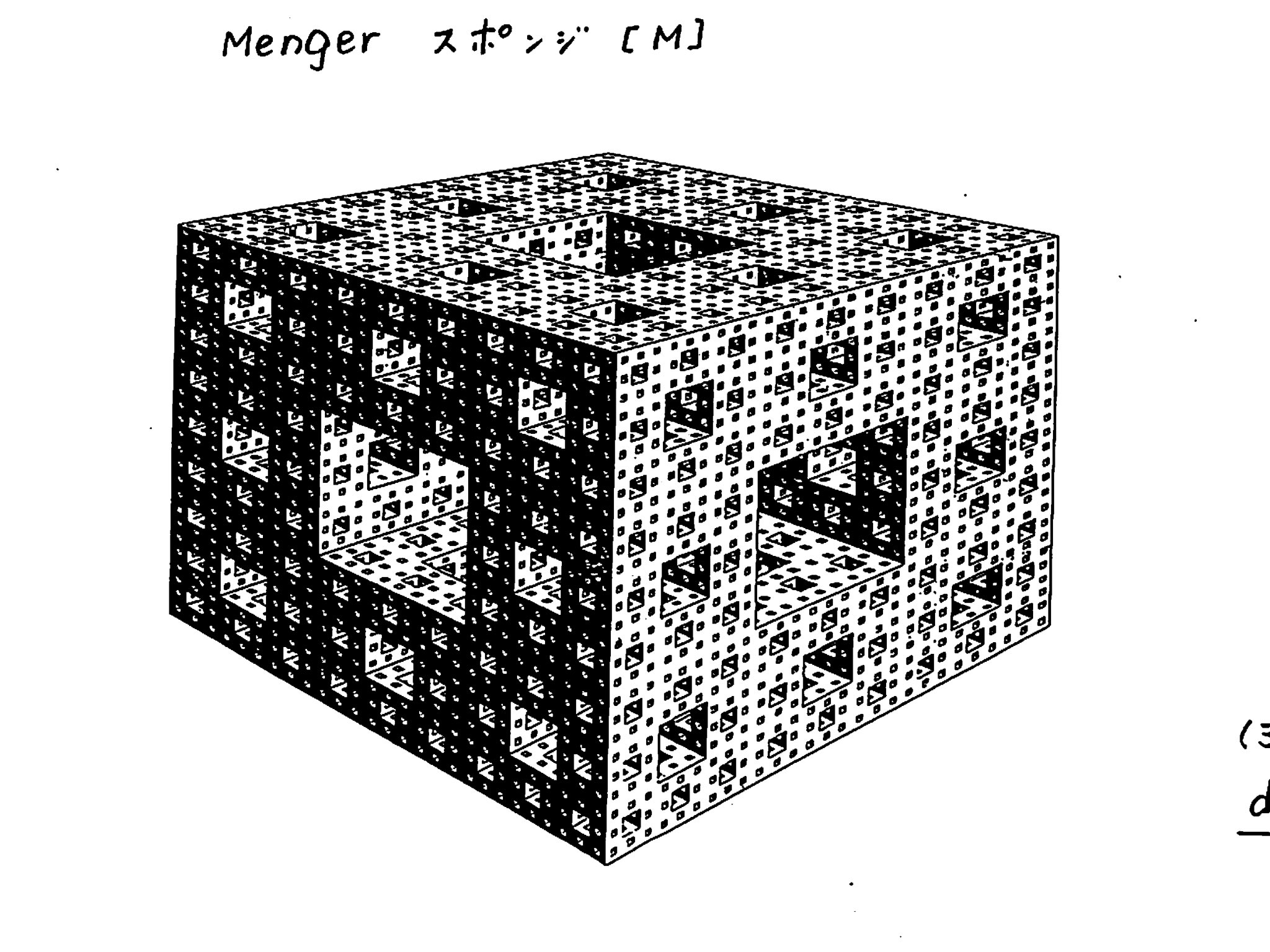


Twitter पर 首都大の猫kumikohattori著書 数学のための英語教本 フラクタル11 メンガーのスポンジ 立方体の各面の中心に辺の長さ1 3の正方形の穴を貫通させて作る フラクタル次元log Log 3 2 72 図はマンデルブロ



Houdini入門しました Gam0022 Net



ねぎパン Negipan Best Friends Chat Best Friends



3dフラクタルで作られた ハイになりそうなミュージックビデオ ギズモード ジャパン



正解するカドの カド をレイマーチングでリアルタイム描画する Gam0022 Net



人気の メンガーのスポンジ 動画 4本 ニコニコ動画



初心者がreactでglslを使う Cloud Config Tech Blog



Draw Menger Sponge メンガーのスポンジの描画 Youtube



Mit Nasaの研究者も熱狂 美しき モダン折り紙 の世界 クーリエ ジャポン


Three000


Minecraft Briefing


折り紙 メンガースポンジ


キュービクスの配色で同時に3タイプ挑戦 折り紙ジャンキー Origami Junkie



Nc Art Project 3 ゲームデータが創り出すアート



Amazon ソファ装飾クリスマスギフトの枕クッションleaning On 3dメンガースポンジ枕カスタム 4545 Cm 1818inch Mediumサイズ450 G 1lb 枕 枕内部は含ま 枕 抱き枕 オンライン通販



みたにっき はてな



メンジャースポンジ 3dモデル 45 Obj Fbx Dxf 3ds Max Free3d



Parametric And Procedural Design With Houdini Houdini Live 007 Menger Sponge Facebook



メンガーのスポンジ スチャラカでスーダラな日々



商品開発vtuberは便利グッズで世界を面白くする Vchase



フラクタルが熱い みんなが呟くフラクタルとは 2ページ目 Togetter
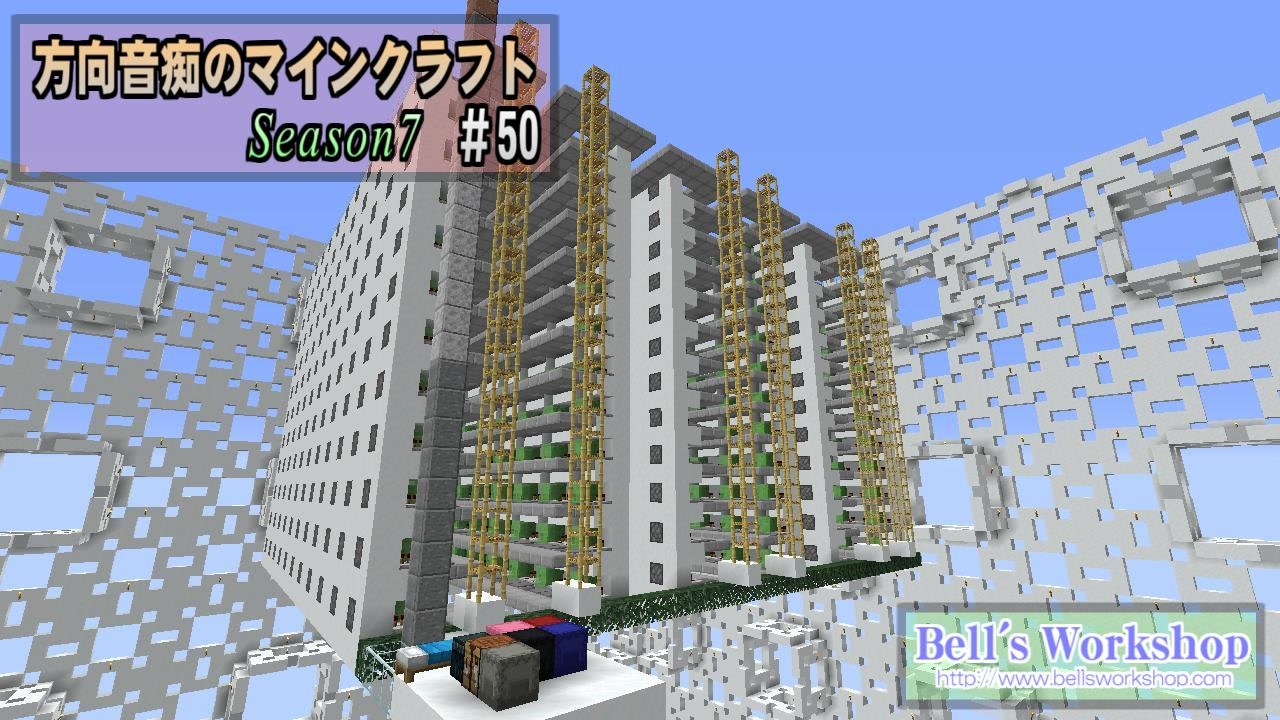


人気の 今日のメンガーさん 動画 29本 ニコニコ動画


45 園部式と専用ユニットによるメンガースポンジ比較 Chimecocoのブログ



Season7 Part70 投稿しました メンガーのスポンジ 完成



メンガーのスポンジ Wikipedia



メンガーのスポンジ



メンガーのスポンジ



メンガー スポンジ 折り紙 作り方



メンガーのスポンジ みたにっき はてな



折紙 メンガーのスポンジlv 2 日常



Amazon Mtbblock Mathtime教育玩具diyおもちゃand Stem Toy For Children Lクリエイティブ学習の数学の図を使用して磁気ブロック アンチ メンガースポンジlevel1セット ままごと ごっこ遊び おもちゃ



Instagramにprocessingで作った作品を投稿し始めて半年たった 備忘録



メンガーのスポンジチャレンジ


最高のマインクラフト 最高スポンジ マイクラ



最高のマインクラフト 最高スポンジ マイクラ



Amazon Mtbblock Mathtime教育玩具diyおもちゃand Stem Toy For Children Lクリエイティブ学習の数学の図を使用して磁気ブロック アンチ メンガースポンジlevel1セット ままごと ごっこ遊び おもちゃ



灯 در توییتر フラクタル図形の一種 メンガー スポンジ のイメージ画像です 面の1 3の正方形をx軸 Y軸 Z軸の3方向にくりぬく操作を無限に繰り返して 限りなくスカスカにしたものです 約2 7次元 表面積無限大 体積0の不思議なものになります Http T Co



Java Edition w14 Minecraft Wiki



三谷 純 Jun Mitani メンガーのスポンジ 関係で本日ツイートした画像13枚を ブログの方にまとめておきました メンガーのスポンジ みたにっき はてな T Co Mywcvy1ocr



3dモデル メンガーのスポンジ Fbx Megalo Arms Corp Booth



Minecraft 方向音痴のマインクラフト Season6 Part61 ゆっくり実況 Youtube



頭がボーっとしてくるフラクタル図形を見よう



メンガーのスポンジの背景 の写真素材 画像素材 Image



メンガーのスポンジの背景 の写真素材 画像素材 Image



Ghp Prog Raham


Yusuke Ogata Celestial Body7 16年11月10日のお気に入り ツイセーブ


数学に女子 寸毫に数話 らぷたん日記 ゚d゚


Yusuke Ogata Celestial Body7 16年11月10日のお気に入り ツイセーブ



首都大の猫kumikohattori著書 数学のための英語教本 A Twitter フラクタル 11 メンガーのスポンジは数学セミナーの表紙にもありました



メンジャースポンジmht 01 3dモデル 15 Obj Fbx Max Free3d


Gdl作品発表会 11 Hlab



Miyabi Sur Twitter メンガーのスポンジ Lv 1 Worldorigamidays 折り紙作品 長方形タント1224枚より T Co Engvjcepd2



3dフラクタル メンガースポンジ Youtube



頭がボーっとしてくるフラクタル図形を見よう


人気の 今日のメンガーさん 動画 29本 ニコニコ動画


カンバスたれ 計算機



フラクタル


Icarus Online



メンジャースポンジ 3dモデル 45 Obj Fbx Dxf 3ds Max Free3d



建設 フラクタル カオス Pixabayの無料画像



コメント
コメントを投稿